近日,女王调教-女王调教视频-女王 调教小说
在色展同伦论中取得重要突破,系列成果发表于《Geometry & Topology》和《Peking Mathematical Journal》。
高阶实K理论是拓扑实K理论在色展同伦中的推广,作为稳定同伦论中的核心研究对象之一,它的同伦群揭示了球面稳定同伦群中的深刻周期现象,并具有重要的几何应用。2016年,Hill—Hopkins—Ravenel通过研究8阶循环子群 $C_8$ 作用下的4阶实K理论 $E_4^{hc_8}$,成功解决了Kervaire不变量问题,并因此获得2022年Veblen几何奖。
同伦不动点谱序列与切片谱序列是计算高阶实K理论同伦群的关键工具。*女王调教-女王调教视频-女王 调教小说段智鹏讲师与李谷川研究员、时骁霖助理教授合作的论文《Vanishing lines in chromatic homotopy theory》,证明了在有限群和任意高度下,所有此类谱序列均存在一个水平消失线,所有此线以上的元素都将消失,并给出了消失线的精确位置,如图1所示。成果发表于拓扑学领域的顶级期刊《Geometry & Topology》上。这一结果是色展同伦理论中的重要突破,既有深刻的理论意义,也为实际计算提供了指导。
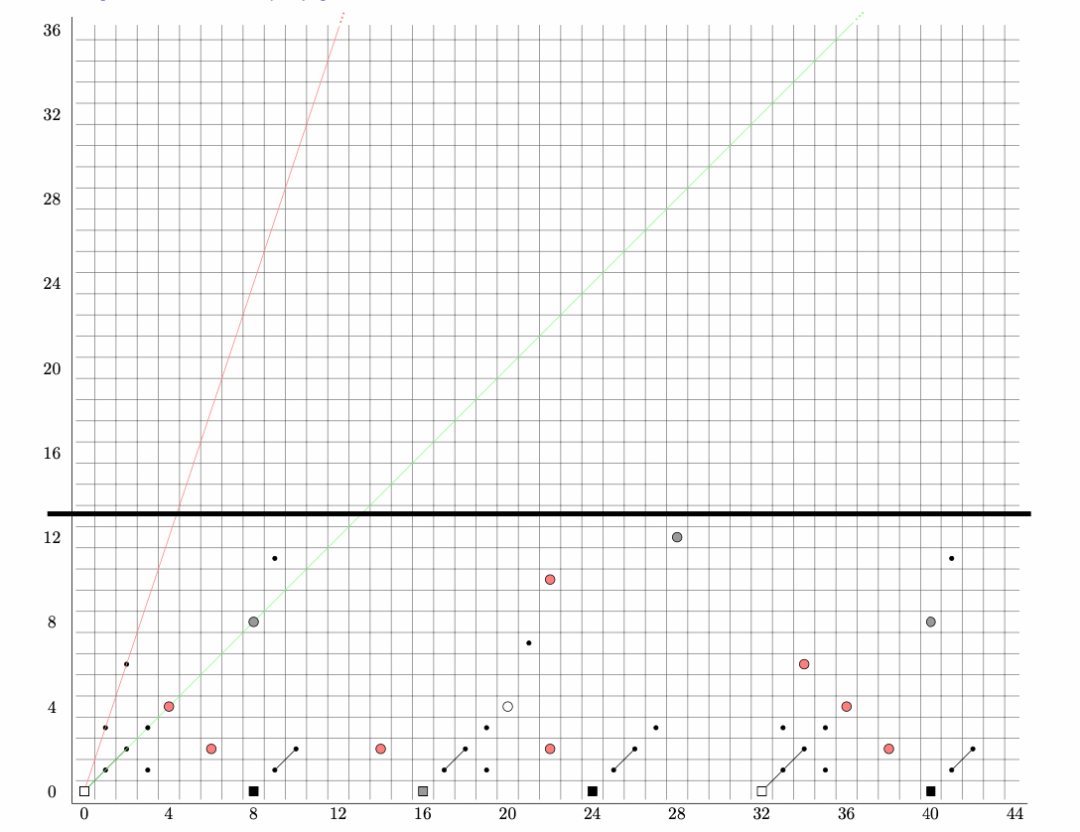
图 1 $E_2^{hc_4}$ 计算的消失线
利用这一结论,段智鹏与孔嘉、李谷川、卢运则和王国祯合作,在题为《RO(G)-Graded Homotopy Fixed Point Spectral Sequence for Height 2 Morava E-Theory》的论文中,成功计算了 $E_2^{hc_8}$ 的同伦群,这是色展同伦理论中非交换群情形下的首次完整计算。该论文发表于《Peking Mathematical Journal》。
相关论文链接:
Vanishing lines in chromatic homotopy theory://msp.org/gt/2025/29-2/gt-v29-n2-p07-p.pdf
RO(G)-Graded Homotopy Fixed Point Spectral Sequence for
Height 2 Morava E-Theory://link.springer.com/article
/10.1007/s42543-024-00087-7